

Apakah kamu pernah memperhatikan lemari yang ada di kamarmu? Seperti apa bentuknya? Lemari yang biasa kamu gunakan untuk menyimpan baju dan mainan itu adalah contoh nyata dari bangun ruang. Bangun ruang adalah bentuk tiga dimensi yang memiliki panjang, lebar, dan tinggi. Bangun ruang menempati volume dalam ruang dan memiliki sifat-sifat seperti luas permukaan, volume, dan bisa juga memiliki sifat lain seperti jumlah sisi, jumlah titik sudut, dan jumlah rusuk.
Beberapa contoh bangun ruang yang umum dikenal adalah:
Setiap bangun ruang ini punya cara khusus untuk menghitung seberapa besar permukaannya dan seberapa banyak ruang di dalamnya. Di artikel ini, kita akan belajar mengenal berbagai macam bangun ruang beserta rumus untuk menghitung luas permukaan dan volumenya
Kubus adalah bangun ruang tiga dimensi yang terdiri dari 6 sisi (3 pasang) yang memiliki ukuran dan bentuk yang sama dan saling berhadapan. Sisi kubus terletak di samping kiri dan kanan, atas dan bawah, serta depan dan belakang. Selain itu, kubus memiliki 12 rusuk dan 8 titik sudut yang merupakan pertemuan dari rusuk-rusuk kubus.

Untuk mencari volume kubus yaitu dengan mengkalikan sisinya atau rusuknya :
Volume kubus = sisi x sisi x sisi
volume kubus = rusuk x rusuk x rusuk
Volume kubus = s³
volume kubus = r³
Untuk mencari luas kubus yaitu :
Luas kubus = 6 x sisi x sisi
luas kubus = 6 x rusuk x rusuk
Luas kubus = 6 x s²
luas kubus = 6 x r²

Perhatikan gambar kubus ABCD.EFGH di atas. Berapakah volume dan luas kubus tersebut?
Jawaban:
Diketahui panjang sisi = 7 cm
Volume kubus ABCD.EFGH = s x s x s
Volume kubus ABCD.EFGH = 7 cm x 7 cm x 7 cm
Volume kubus ABCD.EFGH = 343 cm³
Luas kubus ABCD.EFGH = 6 x s x s
Luas kubus ABCD.EFGH = 6 x 7 cm x 7 cm
Luas kubus ABCD.EFGH = 294 cm²

Balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi panjang dengan satu pasang diantaranya berukuran beda.

Untuk mencari volume kubus yaitu dengan mengkalikan sisinya atau rusuknya :
Volume balok = (2 x panjang x lebar) + (2 x panjang x tinggi) + (2 x lebar x tinggi)
Volume balok = (2 x p x l) + (2 x p x t) + ( 2 x l x t)
Sedangkan rumus luas balok adalah :
Luas balok = panjang x lebar x tinggi
Luas balok = p x l x t

Berapakah volume dan luas dari balok ABCD.EFGH di atas?
Jawaban:
Diketahui :
Volume balok ABCD.EFGH = (2 x p x l) + (2 x p x t) + ( 2 x l x t)
Volume balok ABCD.EFGH = (2 x 10 cm x 6 cm) + (2 x 10 cm x 7 cm) + (2 x 6 cm x 7 cm)
Volume balok ABCD.EFGH = 120 cm + 140 cm + 84 cm
Volume balok ABCD.EFGH = 344 cm³
Luas balok ABCD.EFGH = p x l x t
Luas balok ABCD.EFGH = 10 cm x 6 cm x 7 cm
Luas balok ABCD.EFGH = 420 cm²

Limas segi empat adalah bangun ruang tiga dimensi yang terdiri dari empat buah segitiga yang kongruen dengan satu titik sudut persekutuan dan sebuah alas berbentuk segi empat.

Rumus yang digunakan untuk mencari volume limas segi empat adalah :
Volume limas segi empat = 1/3 x luas alas x tinggi limas
Volume limas segi empat = 1/3 x ( sisi x sisi ) x tinggi limas
Untuk mencari luas permukaan limas segi empat yaitu :
Luas limas segi empat = luas alas + jumlah luas sisi tegak
Luas limas segi empat = ( sisi x sisi ) + 4 (1/2 x alas x tinggi)

Berapakah volume dan luas permukaan limas segi empat ABCD di atas?
Jawaban:
Diketahui :
Volume limas segi empat ABCD = 1/3 x ( sisi x sisi ) x tinggi limas
Volume limas segi empat ABCD = 1/3 x ( 8 cm x 8 cm ) x 6 cm
Volume limas segi empat ABCD = 1/3 x 64 cm x 6 cm
Volume limas segi empat ABCD = 128 cm³
Luas limas segi empat ABCD = luas alas + jumlah luas sisi tegak
Luas limas segi empat ABCD = (sisi x sisi) + 4 (1/2 x alas x tinggi)
Luas limas segi empat ABCD = 8 cm x 8 cm + 4 (1/2 x 8 cm x 7 cm)
Luas limas segi empat ABCD = 64 cm+ 4 (28 cm)
Luas limas segi empat ABCD = 64 cm + 112 cm
Luas limas segi empat ABCD = 176 cm²

Prisma segitiga adalah bangun ruang tiga dimensi yang memiliki alas dan atap berbentuk segitiga. Selain itu, memiliki 5 buah sisi, 9 buah rusuk, 6 buah titik sudut, sisi tegaknya berbentuk segi empat dengan rusuk tegak yang sama panjang.

Untuk mencari volume prisma segitiga yaitu :
Volume prisma segitiga = luas alas x tinggi prisma
Volume prisma segitiga = (1/2 x alas x tinggi) x tinggi prisma
Untuk mencari luas prisma segitiga yaitu :
Luas prisma segitiga = ( 2 x luas alas ) + ( keliling alas x tinggi )
Luas prisma segitiga = { 2 x (1/2 x alas x tinggi )} + ( keliling alas x tinggi )

Perhatikan gambar prisma segitiga ABC.DEF di atas. Hitunglah volume dan luasnya!
Jawaban:
Diketahui :
Volume prisma segitiga ABC.DEF = (1/2 x alas x tinggi) x tinggi prisma
Volume prisma segitiga ABC.DEF = (1/2 x 5 cm x 6 cm) x 10 cm
Volume prisma segitiga ABC.DEF = 150 cm³
Luas alas = ½ x alas x tinggi
Luas alas = ½ x 5 cm x 6 cm
Luas alas = 15 cm²
Keliling alas = sisi + sisi + sisi
Keliling alas = 5 cm + 5 cm + 5 cm
Keliling alas = 15 cm
Luas prisma segitiga ABC.DEF = ( 2 x luas alas ) + ( keliling alas x tinggi )
Luas prisma segitiga ABC.DEF = ( 2 x 15 cm²) + ( 15 cm x 10 cm)
Luas prisma segitiga ABC.DEF = 30 cm² + 150 cm
Luas prisma segitiga ABC.DEF = 180 cm²

Limas segitiga adalah bangun ruang tiga dimensi yang terdiri dari tiga buah segitiga dengan sebuah alas berbentuk segitiga juga. Selain itu memiliki 4 buah sisi, 6 buah rusuk, dan 4 titik sudut.

Rumus volume dan luas limas segitiga yaitu :
Volume limas segitiga = 1/3 x luas alas x tinggi limas
Volume limas segitiga = 1/3 x (1/2 x alas x tinggi) x tinggi limas
Untuk mencari luas limas segitiga yaitu :
Luas limas segitiga = luas alas + jumlah luas sisi tegak
Luas limas segitiga = (1/2 x alas x tinggi) + 3 (1/2 x alas x tinggi)
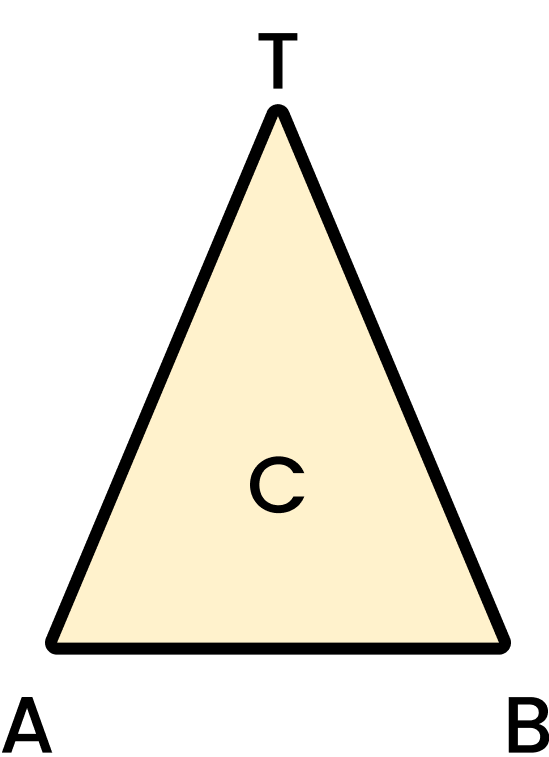
Perhatikan gambar di atas. Hitunglah volume dan luas limas segitiga ABC tersebut!
Jawaban:
Diketahui :
Volume limas segitiga ABC = 1/3 x luas alas x tinggi limas
Volume limas segitiga ABC = 1/3 x (1/2 x alas x tinggi) x tinggi limas
Volume limas segitiga ABC = 1/3 x (1/2 x 7 cm x 6 cm) x 8 cm
Volume limas segitiga ABC = 56 cm³
Luas limas segitiga ABC = luas alas + jumlah luas sisi tegak
Luas limas segitiga ABC = (1/2 x alas x tinggi) + 3 (1/2 x alas x tinggi)
Luas limas segitiga ABC = (1/2 x 7 cm x 6 cm) + 3 (1/2 x 7 cm x 10 cm)
Luas limas segitiga ABC = 21 cm + 3 (105 cm)
Luas limas segitiga ABC = 336 cm²

Silinder atau tabung adalah bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaran yang sejajar dan sebuah persegi panjang yang mengelilingi lingkaran tersebut.

Untuk menghitung volume tabung cukup mengalikan luas alas dan tinggi :
Volume tabung = phi x jari-jari x tinggi
Volume tabung = π x r² x t
Untuk mencari luas keseluruhan tabung, kita perlu menjumlahkan luas dua lingkaran (sisi atas/tutup dan sisi alas) dan luas satu persegi panjang yaitu :
Luas lingkaran (sisi atas/tutup) = π x r²
Luas lingkaran (sisi alas) = π x r²
Luas persegi panjang (selimut) = 2 x π x r x t
Luas tabung = luas lingkaran + luas persegi panjang
Luas tabung = (2 x π x r²) + (2 x π x r x t)
Luas tabung = 2 x π x r (r + t)

Hitunglah volume dan luas tabung di atas!
Jawaban:
Diketahui :
Volume tabung = π x r² x t
Volume tabung = 3,14 x (15 cm)² x 30 cm
Volume tabung = 3,13 x 225 cm x 30 cm
Volume tabung = 21.195 cm³
Luas tabung = 2 x π x r (r + t)
Luas tabung = 2 x 3,14 x 15 cm (15 cm + 30 cm)
Luas tabung = 94,2 cm (45 cm)
Luas tabung = 4.239 cm²

Kerucut adalah limas istemewa dengan alas berbentuk lingkaran, memiliki satu titik puncak dan sisi tegak kerucut tidak berupa segitiga tapi bidang miring atau sisi lengkung yang disebut selimut kerucut.

Rumus volume kerucut yaitu :
Volume kerucut = 1/3 x π x r² x t
Sedangkan rumus luas kerucut yaitu dengan menjumlahkan luas alas dan luas selimut :
Luas alas = π x r²
Luas selimut = π x r x s
Sedangkan rumus luas kerucut yaitu dengan menjumlahkan luas alas dan luas selimut :
Garis pelukis (s) = √r²+ t².
Sehingga rumus luas kerucut adalah :
Luas kerucut = (π x r²) + (π x r x s)
Luas kerucut = π x r (r + s)

Perhatikan gambar kerucut di atas. Hitunglah volume dan luasnya!
Jawaban:
Diketahui :
Volume kerucut = 1/3 x π x r² x t
Volume kerucut = 1/3 x 3,14 x (15 cm)² x 30 cm
Volume kerucut = 1/3 x 3,14 x 225 cm x 30 cm
Volume kerucut = 7.065 cm³
Luas kerucut = π x r (r + s)
Luas kerucut = 3,14 x 15 cm (15 cm + 35 cm)
Luas kerucut = 3,14 x 15 cm (50 cm)
Luas kerucut = 2.355 cm²

Bola adalah bangun ruang tiga dimensi yang terdiri dari sisi lengkung sehingga tidak memiliki rusuk maupun sudut.

Rumus volume dan luas bola yaitu :
Volume bola = 4/3 x π x r³
Untuk mengetahui luas bola yaitu :
Luas bola = 4/3 x π x r²
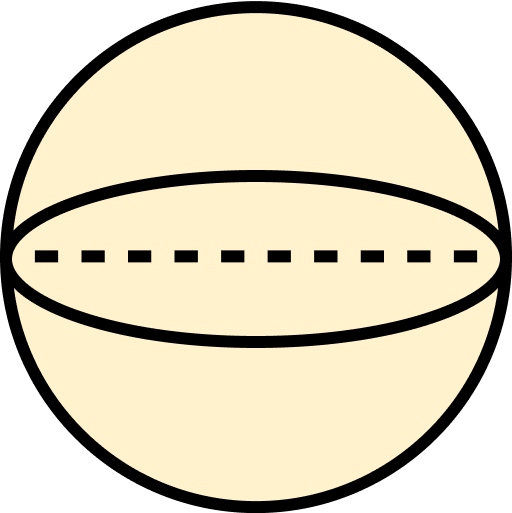
Hitunglah volume dan luas bola di atas!
Jawaban:
Diketahui :
Volume bola = 4/3 x π x r³
Volume bola = 4/3 x 3,14 x (8 cm)³
Volume bola = 4/3 x 3,14 x (512 cm)
Volume bola = 2.143,57 cm³
Luas bola = 4/3 x π x r²
Luas bola = 4/3 x 3,14 x (8 cm)²
Luas bola = 4/3 x 3,14 x (64 cm)
Luas bola = 267,94 cm²

Nah, itulah penjelasan tentang bangun ruang. Sekarang, kamu sudah tahu apa itu bangun ruang, contohnya, dan bagaimana menghitung volume dan luas permukaannya.